My core expertise is quantitative modeling. I work on problems of cell division, mechanics of hearing, and musical instruments. This includes analysis of experimental raw data, numerical modeling, and mathematical descriptions. For me, it is important to have a close connection to the original observation and a careful handling of all intermediate steps up to the discovered scientific statement.

Hearing mechanics
Our hearing organ is able to detect air vibrations with an amplitude smaller than the atomic Bohr radius while cycling about a thousand times per second.
Together with Mario Fleischer, I developed a novel approach to analyze the mechanics of the fluid-structure interaction problem in the inner ear. Because the motions during the normal hearing are smaller than the geometrical scales, a unified linear system of equations describes with sufficient accuracy the behavior of the liquid and solid in terms of a displacement variable. The finite-element method allows us to solve this system of partial differential equations on complex geometries. Based on experimental observations, a detailed model is constructed that resolves different scales and captures known geometrical details.
Finite-element model to analyze the mechanics of the hair bundle in the liquid environment

Each hair bundle comprises many apposed cylindrical stereocilia that are located in a liquid-filled compartment of the inner ear. The viscous liquid surrounding the hair bundle dissipates energy and dampens oscillations, which poses a fundamental physical challenge to the high sensitivity and sharp frequency selectivity of hearing. To understand the structure-function relationship in this complex system, a realistic physical model of the hair bundle with an appropriate representation of the fluid-structure interactions is used to identify the relevant physical effects.
This project was the subject of my PhD thesis under the supervision of Roger Grundmann. I worked on this with Andrei Kozlov, Thomas Risler, Corstiaen P.C. Versteegh, and A.J. Hudspeth.
Finite-element model of the active organ of Corti
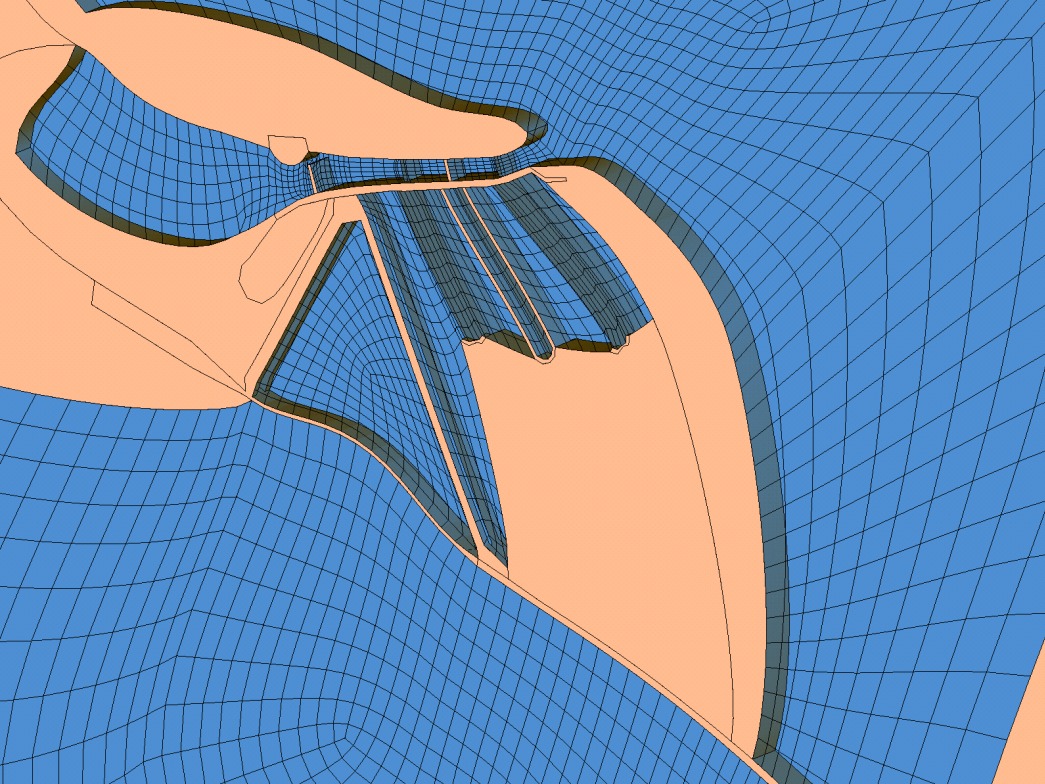
The cochlear amplifier that provides our hearing with its extraordinary sensitivity and selectivity is thought to be the result of an active biomechanical process within the organ of Corti. Although imaging techniques are developing rapidly, it is not currently possible to obtain detailed measurements of the motion of individual elements within a cross-section of the organ of Corti. This motion we predict using a passive two-dimensional finite-element model with an electromechanical feedback system. This allows us to incorporate knowledge about the geometrical arrangement of the various cell types. These are modeled using elastic elements, except the outer hair cells as piezoelectric elements and the perilymph and endolymph as viscous and nearly incompressible fluid elements. The fully active response of the basilar membrane to acoustic excitation is predicted.
Together with Anthony W. Gummer, Manuela Nowotny, Caio Chiaradia, H.-J. Hardtke, Mario Fleischer, Rolf Schmidt, Thomas Zahnert, and Yuri Yarin I started on this subject. In the meantime, Manuela Nowotny started her own group. Recently I coupled the model with an active model together with Steve Elliott and Guangjian Ni.
From the incoming sound to the traveling wave in the cochlea
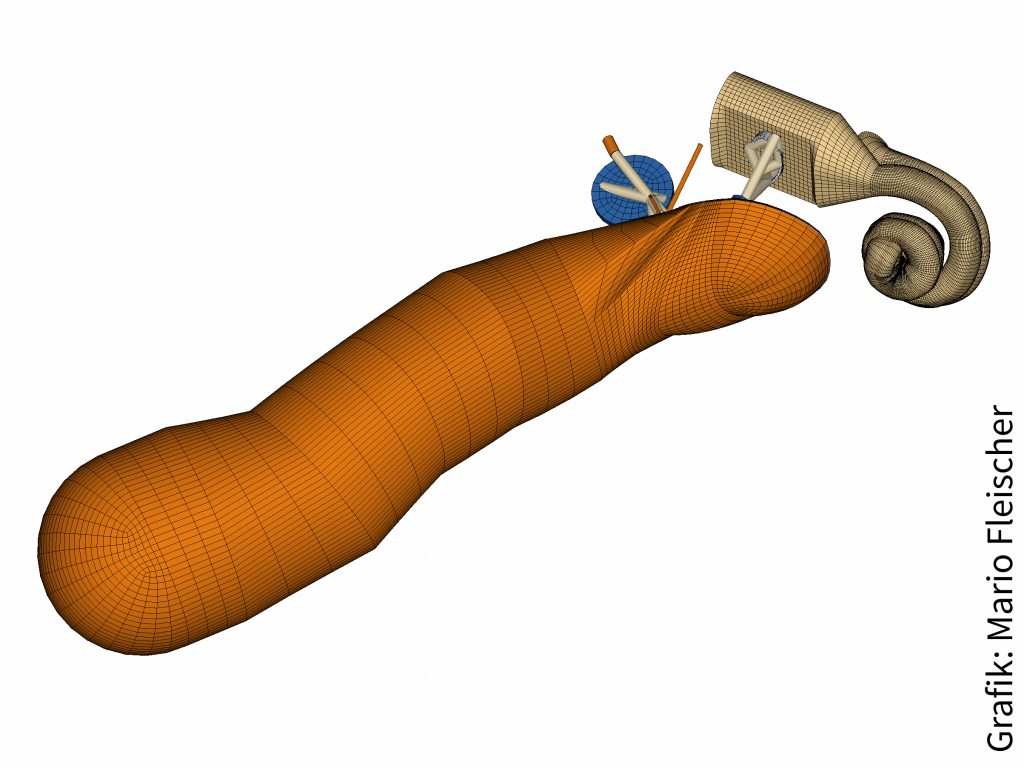
We study the mechanics of the traveling wave by a detailed three-dimensional finite-element model. The model is based on geometry data from μCT-scans of a human ear and the mechanical properties of the basilar membrane are adjusted to ensure the known tonotopic map. Furthermore, we ensure that the orthotropic material of the basilar membrane has a compressibility similar to water. In the current version of the model, we omit the organ of Corti with its various cell types but add a model of the middle ear and the ear canal filled with an acoustic fluid and attached infinite elements to represent the outer ear. This model allows us to compare different load cases and we analyzed for them forces and motions.
The geometry of the human cochlea and the middle ear model is thanks to a collaboration with Thomas Zahnert and Yuri Yarin. With Mario Fleischer and Charles Steele, we adjust the material properties of the model to match known experimental quantitative data.
Musical instruments
Control of the tuning while playing the bassoon

In reed woodwinds, the pitch of a sound is the result of an interaction between the air column, the reed, and the player. The air column is well described by its resonance frequencies and their damping. The reed is a pressure-controlled valve, which drives a coupled oscillation that settles with a fundamental frequency near a resonance frequency of the air column. The musician provides the blowing pressure and can alter the dynamical properties of the reed with his embouchure.
For a musician, it is crucial to adjust the dynamic level while playing in tune. A bassoon player has two major means of control: the mouth pressure and the lip force. In an experimental study, we investigated from the player’s perspective the tuning quality of the entire system under playing conditions. We focus on the lip force a musician has to exert for the instrument to play in tune in two ways. Firstly, a professional musician has been asked to play notes without embouchure corrections on three bassoons. Secondly, the lip force and blowing pressure to play notes in tune were measured on these bassoons with an artificial mouth.
This project is published here. The construction of the artificial mouth and experimental work was a part of the PhD thesis of Timo Grothe.
Modeling of the impedance and sounding frequency of wind instruments
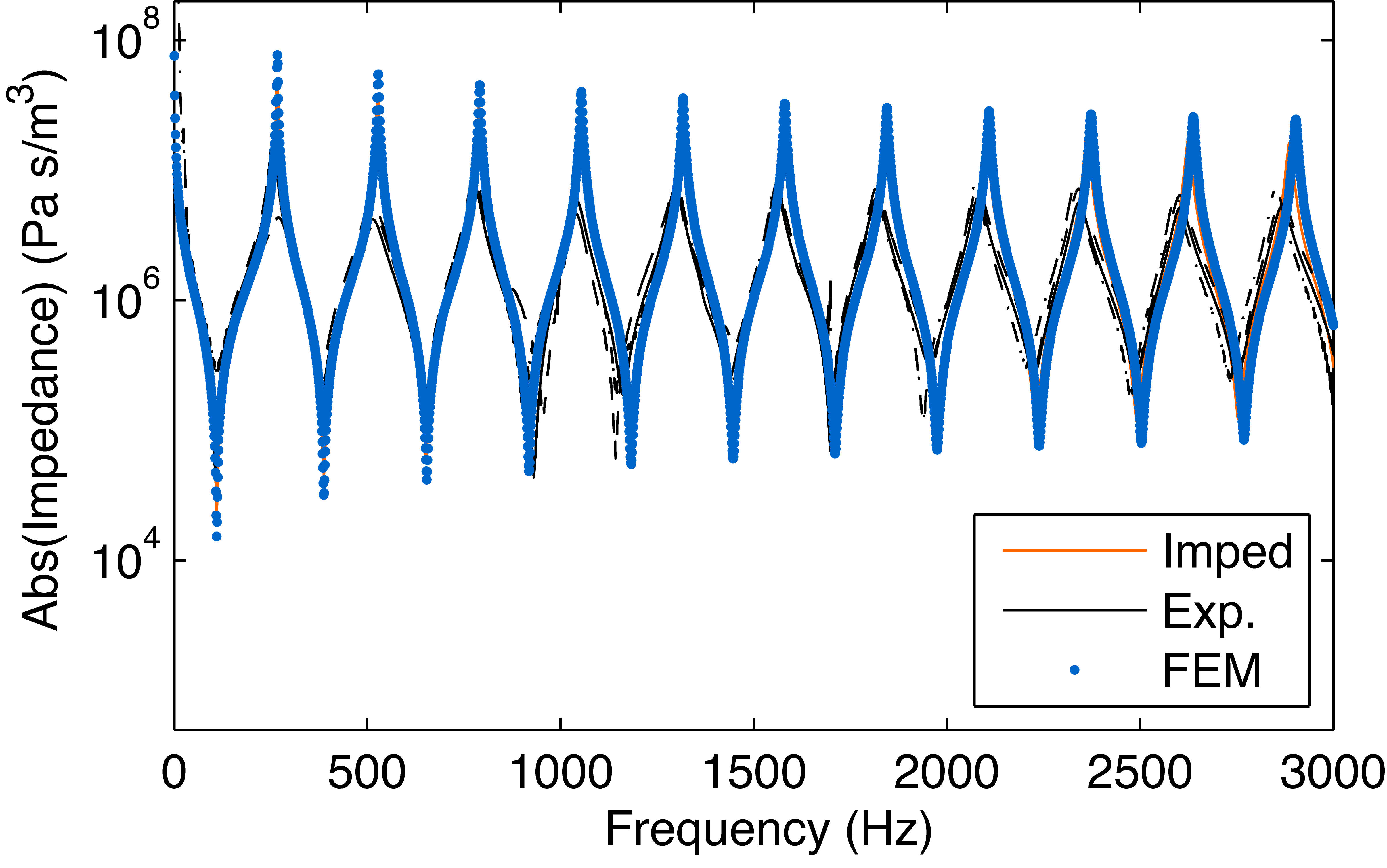
The bore and tone hole geometry of reed woodwinds determine their intonation properties to a large extent. Acoustical modal frequencies of the air-column can be calculated from the geometry with high accuracy. However, the prediction of sounding frequencies from the air column modes is difficult because the reed’s dynamic behavior modifies non-linearly the sounding frequency. This complex coupling with the reed mouthpiece results in significant pitch deviations from the fundamental air column frequency.
To handle this complex problem we rely on two type of models: impedance modeling to characterize the acoustic properties of the resonator and non-linear model including the mouthpiece to estimate the sounding frequency. For the acoustics, we use transmission-line models and detailed three-dimensional finite-element models. The non-linear models are coupled to the impedance studies as well as to measured data. We include here also higher modes, which are especially important for notes in the low range.
This project started at the Technische Universität Dresden in the group of Roger Grundmann with Andreas Richter. Currently, this is continued with Timo Grothe and Cornelis Nederveen.
A complete re-design of the bassoon

The bassoon suffers from a limited dynamic range and the sound color is not very prominent if played in a group of wind instruments. Based on experiments with different opening angles of a bassoon-like geometry we designed a new instrument together with the company Guntram Wolf Holzblasinstrumente GmbH and Benedikt Eppelsheim which is louder and provides more dynamic range than the traditional German bassoon.
For this new invention, a patent (DE201210006123) was granted.
Spindle mechanics
We do not build houses for a century with bricks that have an average lifetime of a year.
The spindle is in this counterintuitive regime and, as such, is both flexible and dynamic.
I conduct my research in the biophysics division at the Max Planck Institute for the Physics of Complex Systems working with Frank Jülicher. I combine data analysis of electron tomography and light microscopy data with numerical simulations and modeling to gain insights into this self-assembly process and the mechanics of the metaphase spindle.
Estimating dynamic properties of microtubules in the spindle

Mass balance allows us to connect the light microscopy picture of the spindle with our knowledge about the building blocks: stiff microtubules, which turnover rapidly. It is so far not possible to track individual microtubules in living samples, as the density is high, the microtubules diffuse around, and the optical quality is poor.
Based on tracking of the growing microtubule tips, marked by EB1-GFP, we were able to show in a perturbation experiment that: XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. The experimental work was mainly performed by Anthony Hyman and Simone Reber. Simone Reber started in the meantime her own lab. The theoretical modeling part and data analysis were conducted by Frank Jülicher and myself.
Tracking individual EB1 tracks in the dense spindle is prone to artifacts. With the lab of Jan Brugués, we work on a new concept of the data analysis based on spatial-temporal correlations. With this approach, we give up on information of individual tracks for the sake of less parameter-dependent tracking method.
The architecture of the metaphase spindle described by the arrangement of microtubules

The poles of the spindle are singularities where the orientation of the microtubules, the main structural component of the spindle, is not well defined. I analyze the local microtubule arrangement to retrieve precise quantitative measures, such as the local density, local ordering, and length distributions.
Large-scale serial electron tomography provides a complete geometrical description of the microtubules in three-dimensional space. The major part of data acquisition was performed by Thomas Müller-Reichert and Stefanie Redemann and by the lab of Anthony Hyman with Jean-Marc Verbavatz. The segmentation of the data was supported by Steffen Prohaska and Norbert Lindow. We gain further insights by incorporating our findings in models together with Jan Brugués and the lab of Michael Shelley with Sebastian Fürthauer and Ehssan Nazockdast.
Our paper C. elegans chromosomes connect to centrosomes by anchoring into the spindle network is available here. Currently, I use this detailed information on local microtubule densities to study the local concentration of tubulin polymerized into microtubules and in solution with Frank Jülicher, Jan Brugués, Anthony Hyman, Jeffrey Woodruff, Jean-Marc Verbavatz, Thomas Müller-Reichert, Marcel Kirchner, Stefanie Redemann, Steffen Prohaska, and Norbert Lindow.
The metaphase spindle as an active liquid-like drop
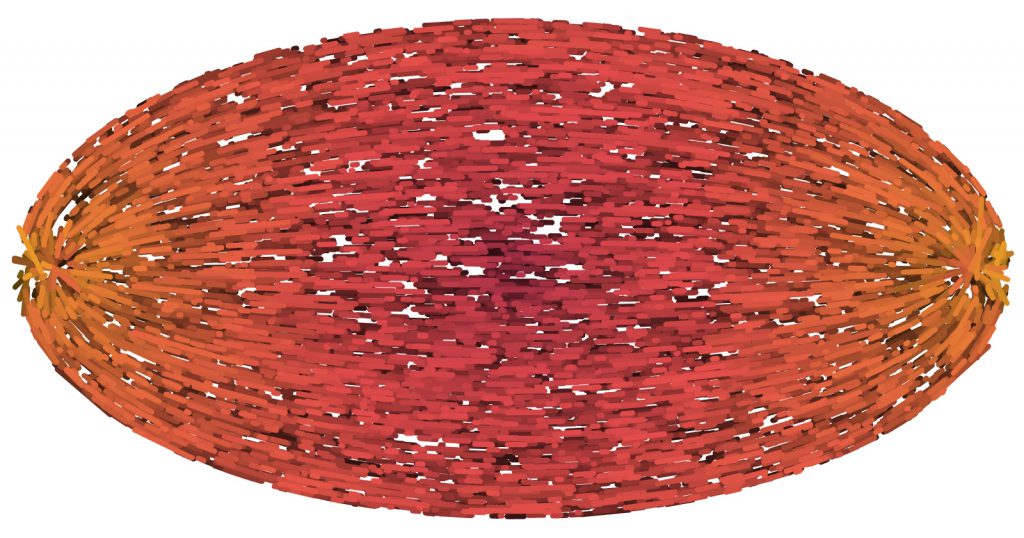
In cells the spindle apparatus reliably segregates chromosomes. The spindle’s main sub-units are hundreds of thousands of dynamic microtubules, which are well-studied. Despite this detailed knowledge, an understanding of how their collective properties give rise to a spindle with a defined size and shape is still lacking. To investigate how the self-organization of microtubules relates to the characteristic shape of the spindle, we use active liquid crystal theory. This approach is motivated by the rapid turnover of microtubules, their steric interactions, and the motor proteins acting between pairs of microtubules.
Such a description allows us to analyze spindle mechanics by nematic field equations in an active fluid. Here, we study a description including the orientation field, active stresses due to motors, and a source term to account for microtubule nucleation. We solve the set of differential equations by means of the finite element method.
On this theoretical project, I work with Frank Jülicher, Jan Brugués, David Oriola, Benjamin Dalton, Jean-François Joanny, and Christoph Erlenkämper.

